Results

1… Fractal Results

Runtime

2… Points in Set vs. Time (Separated)

4… Points in Set vs. Time (Combined)

6… Performance Analysis

7… Task Manager

Performance Model

8… Overall Fractal Performance Model

9… Fractal Performance Model Time Constraints

9… Time Constraints for Fractal Performance Model

12… Solar Sim Results

Runtime

12… Laptop Vs. Cluster Runtime

13… Nodes in Cluster

14… Start Time Analysis

14… Transmission Time Solar Sim

Performance Model

16… Estimated Calculation Time for 3D Solar Sim

16… Performance Model (Solar Sim) Elements

22… Estimated Time for 3D Solar Sim With Multiple Spacecraft per Processor

23… Time Advantage of Adding a Node

29… Cellular Automata Results

Runtime

29…Time to Run 1200x1200 Cellular Automata

Performance Model

30… Transmission and Calculation Time, Cellular Automata

31… Transmission and Calculation Cross Effecting Total Time

Analysis

31… Rate of Change: Derivatives of Calc, Trans, and Total

32… Derivatives of Trans and Calc: Their Effect on Total Time

35… Fractal Pictures

46… Solar Sim Pictures

49… Cluster Pictures

Fractal Results

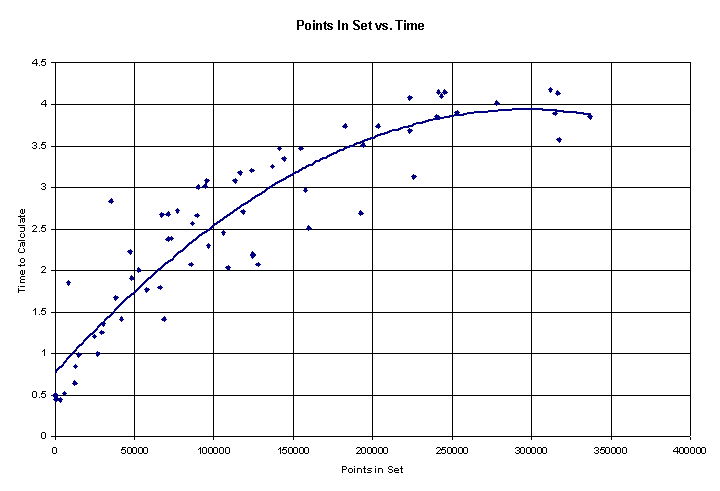
Here are two graphs recording the number of points that were in the Mandelbrot set vs. the time it took to calculate. The first accounts for the entire time vs. the entire number of points. The second shows the three different processors and graphs their points independently. Both include trend graphs, the first is a polynomial and the second is linear.

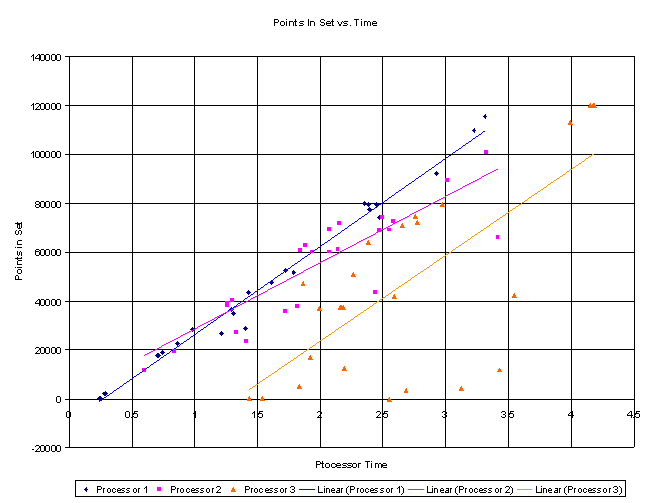This graph shows the relative speeds of each node, a demonstration of the need for node weighting.

time p1	time p2	time p3	pixels p1	pixels p2	pixels p3
0.701	2.073	2.173	17976	69150	37358
0.741	1.262	2.383	18973	38962	64066
0.281	1.302	1.863	2035	40089	47039
0.24	0.601	2.974	66	11487	79449
0.25	0.841	2.774	87	19420	72048
1.292	1.933	3.996	36483	59913	113081
2.394	2.494	4.186	77237	74164	119939
2.453	2.553	4.176	79511	69133	119753
1.793	2.143	4.156	51657	60975	119996
0.711	2.073	2.183	17976	69150	37358
2.353	2.443	2.553	79920	43205	0
1.212	1.332	1.442	26980	27083	133
2.383	2.473	2.593	79518	68692	41919
3.315	3.415	3.545	115437	65992	42327
1.723	1.823	1.923	52522	37857	16776
1.612	1.722	1.832	47675	35736	4772
1.311	1.412	1.542	34798	23572	159
1.402	2.073	2.193	28783	60044	12196
2.474	2.584	2.684	74066	72324	3364
2.924	3.015	3.125	92150	89298	4142
3.225	3.325	3.425	109442	100402	11801
0.701	2.073	2.173	17976	69150	37358
0.981	1.883	1.993	28458	62661	36868
1.432	2.153	2.263	43551	71786	51017
0.701	2.073	2.164	17976	69150	37358
0.291	1.262	2.754	2309	38320	74529
0.861	1.843	2.659	22549	60582	70895

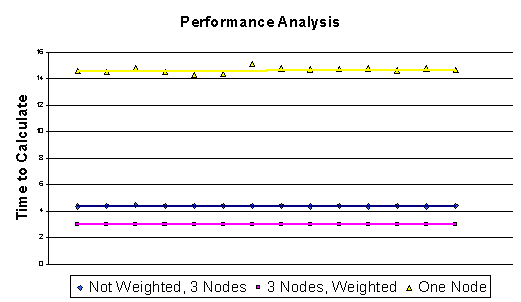
This Graph shows how not weighting the nodes during a fractal run, along with the variability of the program, affects the curve.

pixels	time
124484	2.174
96663	2.293
105763	2.453
85348	2.072
57893	1.763
159885	2.503
127775	2.073
336976	3.856
317507	3.576
225914	3.125
192411	2.684
48047	1.903
116447	3.175
94612	3.014
77301	2.714
67257	2.674
203569	3.735
95629	3.075
35249	2.834
8575	1.853
124484	2.194
68848	1.412
12456	0.641
3466	0.44
303	0.491
544	0.45
1112	0.451
25	0.49
5832	0.511
13036	0.842
241281	4.145
14822	0.981
38512	1.672
52784	2.002
73238	2.383
71133	2.373
86687	2.564
223312	3.676
316594	4.136
315132	3.886
311755	4.176
245226	4.146
223482	4.076
124484	2.173
157627	2.964
118489	2.704
194084	3.505
253344	3.896
278096	4.016
240083	3.856
243181	4.096
47359	2.224
154833	3.475
90133	3.005
71281	2.683
89370	2.664
113366	3.084
137027	3.255
144330	3.345
182494	3.735
124484	2.183
141322	3.475
123799	3.204
27058	0.991
108769	2.033
41838	1.412
66295	1.793
29475	1.252
24693	1.202
30277	1.352

This shows the difference the cluster makes in the calculation and the variability of the fractal calculation.

Comparison of different computers
Standardization:
Left:	-1.5
Right:	0.7
Top:	1
Bottom:	-1
Maxsteps:	254
Numcols:	900
Numrows:	900
One computer, 800 mz	Three nodes, not weighted	weighted, 3 nodes
14.591	4.366	2.964
14.521	4.376	2.974
14.801	4.416	3.024
14.551	4.376	2.964
14.32	4.386	2.984
14.331	4.386	2.974
15.132	4.386	2.964
14.771	4.376	2.964
14.701	4.357	2.975
14.711	4.376	2.975
14.751	4.366	2.974
14.631	4.386	2.965
14.771	4.367	2.975
14.641	4.386	2.964

This page freeze of task manager during a three-year simulation is descriptive of the tasks the
computer carries out during this time.

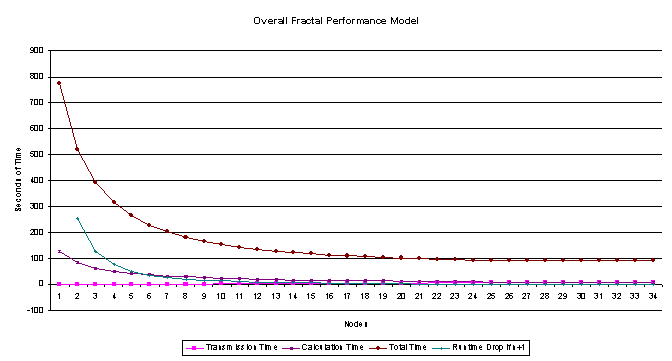
This graph shows the overall result for the fractal performance model.

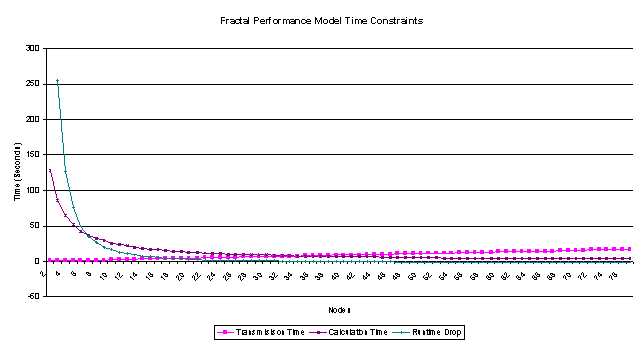
This graph focuses on the effect nodes have on individual time calculations.

This graph shows that happens when the transmission time is greater than the calculation time, making the addition of a node take more time than not adding it.

Data for Fractal Performance Model:

FRACTALS
width	0.002777778
delay=	0.219272727
send time=	0.282181818
p=	640000
calc of one pixel	0.000401498
assumign equally shared between processors

n	trans time is (nodes-1)time delay plus send time	num sims= the negative of the log of desired width over log of scale factor (3)	celing function of the pervious	calc time= (pixels*calc of a pixel) over nodes	total= (trans+calc)*sims
2	0.501455	5.357763	6	128.4792	773.884
3	0.720727	5.357763	6	85.6528	518.2412	255.6428
4	0.94	5.357763	6	64.2396	391.0776	127.1636
5	1.159273	5.357763	6	51.39168	315.3057	75.77189
6	1.378545	5.357763	6	42.8264	265.2297	50.07605
7	1.597818	5.357763	6	36.70834	229.837	35.39271
8	1.817091	5.357763	6	32.1198	203.6214	26.21562
9	2.036364	5.357763	6	28.55093	183.5238	20.09756
10	2.255636	5.357763	6	25.69584	167.7089	15.81492
11	2.474909	5.357763	6	23.35986	155.0086	12.70028
12	2.694182	5.357763	6	21.4132	144.6443	10.36429
13	2.913455	5.357763	6	19.76603	136.0769	8.567379
14	3.132727	5.357763	6	18.35417	128.9214	7.15552
15	3.352	5.357763	6	17.13056	122.8954	6.026033
16	3.571273	5.357763	6	16.0599	117.787	5.108324
17	3.790545	5.357763	6	15.1152	113.4345	4.352564
18	4.009818	5.357763	6	14.27547	109.7117	3.722764
19	4.229091	5.357763	6	13.52413	106.5193	3.192406
20	4.448364	5.357763	6	12.84792	103.7777	2.741602
21	4.667636	5.357763	6	12.23611	101.4225	2.355198
22	4.886909	5.357763	6	11.67993	99.40102	2.021486
23	5.106182	5.357763	6	11.1721	97.66972	1.731301
24	5.325455	5.357763	6	10.7066	96.19233	1.47739
25	5.544727	5.357763	6	10.27834	94.93838	1.253948
26	5.764	5.357763	6	9.883016	93.8821	1.056287
27	5.983273	5.357763	6	9.516978	93.00151	0.880589
28	6.202545	5.357763	6	9.177086	92.27779	0.723716
29	6.421818	5.357763	6	8.860635	91.69472	0.583071
30	6.641091	5.357763	6	8.56528	91.23823	0.456491
31	6.860364	5.357763	6	8.288981	90.89607	0.34216
32	7.079636	5.357763	6	8.02995	90.65752	0.238548
33	7.298909	5.357763	6	7.786619	90.51317	0.144355
34	7.518182	5.357763	6	7.5576	90.45469	0.058473
35	7.737455	5.357763	6	7.341669	90.47474	-0.02005
36	7.956727	5.357763	6	7.137734	90.56677	-0.09202
37	8.176	5.357763	6	6.944822	90.72493	-0.15817
38	8.395273	5.357763	6	6.762063	90.94402	-0.21909
39	8.614545	5.357763	6	6.588677	91.21934	-0.27532
40	8.833818	5.357763	6	6.42396	91.54667	-0.32733
41	9.053091	5.357763	6	6.267278	91.92222	-0.37554
42	9.272364	5.357763	6	6.118057	92.34253	-0.42031
43	9.491636	5.357763	6	5.975777	92.80448	-0.46195
44	9.710909	5.357763	6	5.839964	93.30524	-0.50076
45	9.930182	5.357763	6	5.710187	93.84221	-0.53697
46	10.14945	5.357763	6	5.586052	94.41304	-0.57083
47	10.36873	5.357763	6	5.4672	95.01557	-0.60252
48	10.588	5.357763	6	5.3533	95.6478	-0.63224
49	10.80727	5.357763	6	5.244049	96.30793	-0.66013
50	11.02655	5.357763	6	5.139168	96.99428	-0.68635
51	11.24582	5.357763	6	5.0384	97.70531	-0.71103
52	11.46509	5.357763	6	4.941508	98.43959	-0.73428
53	11.68436	5.357763	6	4.848272	99.19581	-0.75622
54	11.90364	5.357763	6	4.758489	99.97275	-0.77694
55	12.12291	5.357763	6	4.671971	100.7693	-0.79653
56	12.34218	5.357763	6	4.588543	101.5843	-0.81507
57	12.56145	5.357763	6	4.508042	102.417	-0.83263
58	12.78073	5.357763	6	4.430317	103.2663	-0.84929
59	13	5.357763	6	4.355227	104.1314	-0.8651
60	13.21927	5.357763	6	4.28264	105.0115	-0.88011
61	13.43855	5.357763	6	4.212433	105.9059	-0.89439
62	13.65782	5.357763	6	4.144491	106.8139	-0.90798
63	13.87709	5.357763	6	4.078705	107.7348	-0.92092
64	14.09636	5.357763	6	4.014975	108.668	-0.93326
65	14.31564	5.357763	6	3.953206	109.6131	-0.94502
66	14.53491	5.357763	6	3.893309	110.5693	-0.95625
67	14.75418	5.357763	6	3.8352	111.5363	-0.96698
68	14.97345	5.357763	6	3.7788	112.5135	-0.97724
69	15.19273	5.357763	6	3.724035	113.5006	-0.98705
70	15.412	5.357763	6	3.670834	114.497	-0.99643
71	15.63127	5.357763	6	3.619133	115.5024	-1.00543
72	15.85055	5.357763	6	3.568867	116.5165	-1.01404
73	16.06982	5.357763	6	3.519978	117.5388	-1.0223
74	16.28909	5.357763	6	3.472411	118.569	-1.03023
75	16.50836	5.357763	6	3.426112	119.6069	-1.03784
76	16.72764	5.357763	6	3.381032	120.652	-1.04515
77	16.94691	5.357763	6	3.337122	121.7042	-1.05218

Solar Sim Results

This graph shows the relative speeds of a single laptop against the cluster, both running the same Solar Simulation.

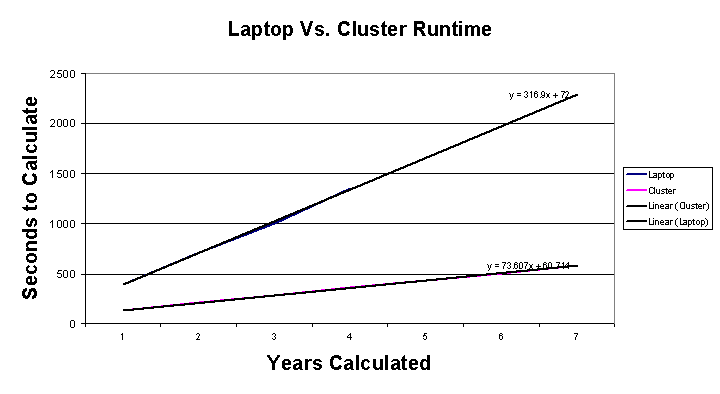
The estimated time you save when using the cluster over the laptop is 243.293x+11.283.

Data:

Laptop	Cluster
392	133
711	208
1003	282
1351	357
	429
	502
	575

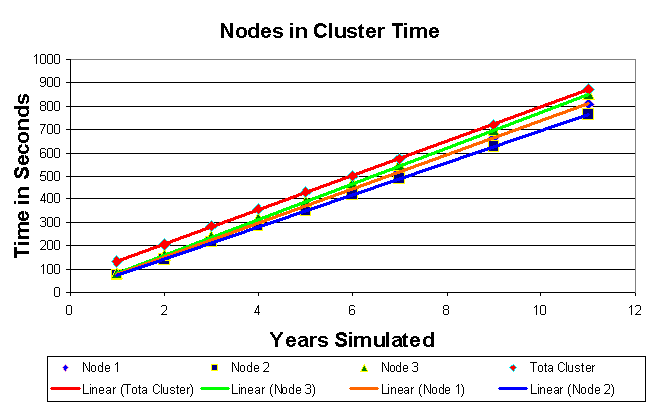
This graph shows the relative speeds of each node, and how they diverge with the number of calculations.

n1	n2	n3	total in sec
78.26	73.51	82.11	133
153.32	143.687	160.872	208
227.147	214.048	239.815	282
302.194	284.079	317.687	357
374.158	352.437	394.137	429
447.203	420.795	470.546	502
519.727	489.244	547.117	575

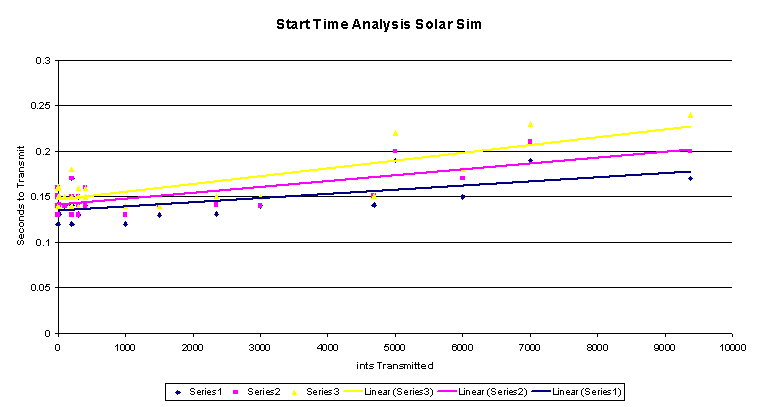
This graph focuses on the startup time of transmission for the smallest possible structure.

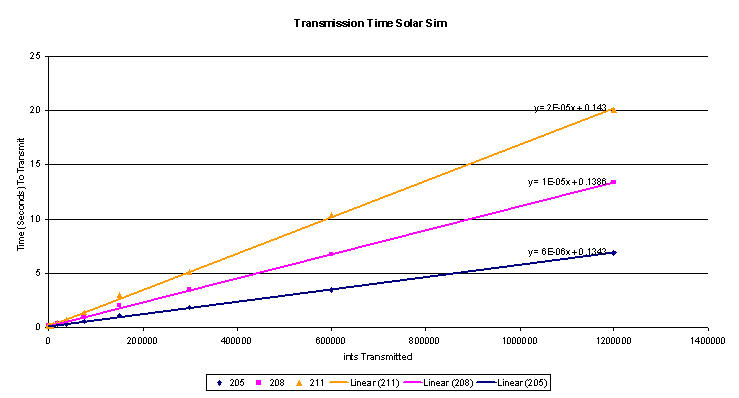
Solar Sim tests of startup time using the minimum possible structure to send.

The second graph extends the transmission analysis to include sending differing amounts of information. Since Solar Sim sends back an integer containing RGB and the rocket ID, the amount of information transmitted is measured in ‘ints’. This allows the estimate of the time to transmit any given amount of data.

Raw data for both graphs:

K1000	timenum for nodes+transfer nide 205	208	211
1	0.13	0.13	0.14
1	0.12	0.14	0.15
1	0.14	0.151	0.161
1	0.15	0.16	0.16
1	0.13	0.14	0.15
2	0.14	0.15	0.16
20	0.131	0.141	0.151
100	0.14	0.14	0.15
200	0.12	0.13	0.14
200	0.14	0.15	0.15
200	0.17	0.17	0.18
300	0.13	0.13	0.14
300	0.15	0.15	0.16
300	0.131	0.141	0.151
400	0.15	0.16	0.16
400	0.14	0.14	0.15
1000	0.12	0.13	0.14
1500	0.13	0.14	0.14
2343	0.131	0.141	0.151
3000	0.14	0.14	0.15
4687	0.141	0.151	0.151
5000	0.19	0.2	0.22
6000	0.15	0.17	0.18
7000	0.19	0.21	0.23
9375	0.17	0.2	0.24
18750	0.24	0.32	0.41
37500	0.31	0.51	0.701
75000	0.541	0.952	1.352
150000	1.062	2.023	3.025
300000	1.873	3.475	5.108
600000	3.475	6.76	10.385
1200000	6.93	13.379	20.099

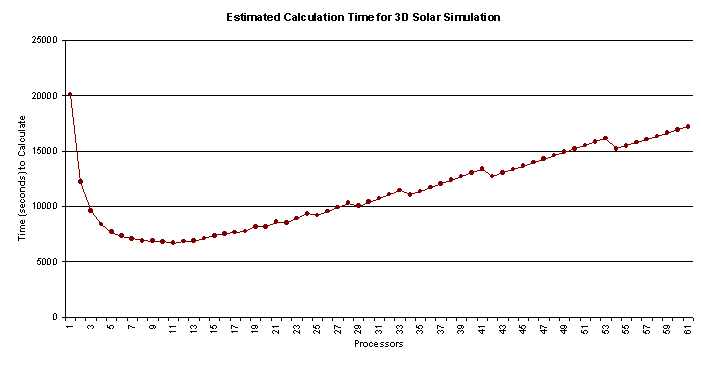
To determine how scalable this system is to large numbers of computers, this graph shows the estimated runtime for Solar Sim using tens of nodes and therefore allowing for 3D simulation.

The graph is not smooth because the number of times needed to repeat the calculation for a desired result cannot be fractional, and so the ceiling function is needed. However, sometimes when one node is added, such as the break between 28 and 29 nodes, the extra node will throw the number of repeats just under a integer, and give an added calculation time decrease to that number of nodes.

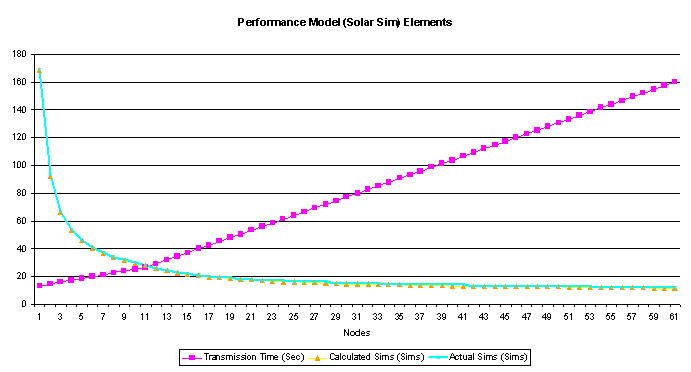
This shows how the variables in the 3D estimate change according to the number of nodes.

Raw data for both Solar Sim 3D performance model with one spacecraft per node:

n	trans time is (nodes-1)time delay plus send time	num sims= the negative of the log of desired width over log of rockets	celing function of the pervious	calc time= number of rockets, aka nodes, times one calc	total= (trans+calc)*sims
2	2.37075	#NUM!	#NUM!	21.2	#NUM!
3	3.7072	#NUM!	#NUM!	31.8	#NUM!
4	5.04365	#NUM!	#NUM!	42.4	#NUM!
5	6.3801	-17.5449	#NUM!	53	#NUM!
6	7.71655	-31.6747	#NUM!	63.6	#NUM!
7	9.053	-57.9146	#NUM!	74.2	#NUM!
8	10.38945	-134.564	#NUM!	84.8	#NUM!
9	11.7259	#DIV/0!	#DIV/0!	95.4	#DIV/0!
10	13.06235	168.4278	169	106	20121.54
11	14.3988	92.07947	93	116.6	12182.89
12	15.73525	66.43667	67	127.2	9576.662
13	17.0717	53.49565	54	137.8	8363.072
14	18.40815	45.65021	46	148.4	7673.175
15	19.7446	40.36195	41	159	7328.529
16	21.08105	36.54121	37	169.6	7055.199
17	22.4175	33.64207	34	180.2	6888.995
18	23.75395	31.3605	32	190.8	6865.726
19	25.0904	29.51362	30	201.4	6794.712
20	26.42685	27.98467	28	212	6675.952
22	29.09975	25.59214	26	233.2	6819.794
24	31.77265	23.7969	24	254.4	6868.144
26	34.44555	22.39303	23	275.6	7131.048
28	37.11845	21.26038	22	296.8	7346.206
30	39.79135	20.32397	21	318	7513.618
32	42.46425	19.53445	20	339.2	7633.285
34	45.13715	18.858	19	360.4	7705.206
36	47.81005	18.2706	19	381.6	8158.791
38	50.48295	17.75471	18	402.8	8159.093
40	53.15585	17.29719	18	424	8588.805
42	55.82875	16.88801	17	445.2	8517.489
44	58.50165	16.51935	17	466.4	8923.328
46	61.17455	16.18505	17	487.6	9329.167
48	63.84745	15.88015	16	508.8	9162.359
50	66.52035	15.60064	16	530	9544.326
52	69.19325	15.34321	16	551.2	9926.292
54	71.86615	15.10513	16	572.4	10308.26
56	74.53905	14.88411	15	593.6	10022.09
58	77.21195	14.67822	15	614.8	10380.18
60	79.88485	14.48582	15	636	10738.27
62	82.55775	14.30551	15	657.2	11096.37
64	85.23065	14.13607	15	678.4	11454.46
66	87.90355	13.97646	14	699.6	11025.05
68	90.57645	13.82575	14	720.8	11359.27
70	93.24935	13.68316	14	742	11693.49
72	95.92225	13.54799	14	763.2	12027.71
74	98.59515	13.41959	14	784.4	12361.93
76	101.2681	13.29744	14	805.6	12696.15
78	103.941	13.18103	14	826.8	13030.37
80	106.6139	13.06993	14	848	13364.59
82	109.2868	12.96374	13	869.2	12720.33
84	111.9597	12.86211	13	890.4	13030.68
86	114.6326	12.76472	13	911.6	13341.02
88	117.3055	12.67127	13	932.8	13651.37
90	119.9784	12.58152	13	954	13961.72
92	122.6513	12.49522	13	975.2	14272.07
94	125.3242	12.41214	13	996.4	14582.41
96	127.9971	12.3321	13	1017.6	14892.76
98	130.67	12.25491	13	1038.8	15203.11
100	133.3429	12.1804	13	1060	15513.46
102	136.0158	12.10842	13	1081.2	15823.8
104	138.6887	12.03883	13	1102.4	16134.15
106	141.3616	11.97149	12	1123.6	15179.54
108	144.0345	11.90629	12	1144.8	15466.01
110	146.7074	11.84311	12	1166	15752.49
112	149.3803	11.78185	12	1187.2	16038.96
114	152.0532	11.72241	12	1208.4	16325.44
116	154.7261	11.6647	12	1229.6	16611.91
118	157.399	11.60864	12	1250.8	16898.39
120	160.0719	11.55415	12	1272	17184.86
122	162.7448	11.50115	12	1293.2	17471.34
124	165.4177	11.44958	12	1314.4	17757.81
126	168.0906	11.39938	12	1335.6	18044.29
128	170.7635	11.35047	12	1356.8	18330.76
130	173.4364	11.30281	12	1378	18617.24
132	176.1093	11.25635	12	1399.2	18903.71
134	178.7822	11.21103	12	1420.4	19190.19
136	181.4551	11.1668	12	1441.6	19476.66
138	184.128	11.12363	12	1462.8	19763.14
140	186.8009	11.08146	12	1484	20049.61
142	189.4738	11.04026	12	1505.2	20336.09
144	192.1467	11	11	1526.4	18904.01
146	194.8196	10.96063	11	1547.6	19166.62
148	197.4925	10.92213	11	1568.8	19429.22
150	200.1654	10.88445	11	1590	19691.82
152	202.8383	10.84758	11	1611.2	19954.42
154	205.5112	10.81148	11	1632.4	20217.02
156	208.1841	10.77612	11	1653.6	20479.62
158	210.857	10.74148	11	1674.8	20742.23
160	213.5299	10.70754	11	1696	21004.83
162	216.2028	10.67427	11	1717.2	21267.43
164	218.8757	10.64164	11	1738.4	21530.03
166	221.5486	10.60964	11	1759.6	21792.63
168	224.2215	10.57825	11	1780.8	22055.24
170	226.8944	10.54745	11	1802	22317.84
172	229.5673	10.51721	11	1823.2	22580.44
174	232.2402	10.48752	11	1844.4	22843.04
176	234.9131	10.45837	11	1865.6	23105.64
178	237.586	10.42974	11	1886.8	23368.25
180	240.2589	10.4016	11	1908	23630.85
182	242.9318	10.37395	11	1929.2	23893.45
184	245.6047	10.34678	11	1950.4	24156.05
186	248.2776	10.32006	11	1971.6	24418.65
188	250.9505	10.29379	11	1992.8	24681.25
190	253.6234	10.26795	11	2014	24943.86
192	256.2963	10.24253	11	2035.2	25206.46
194	258.9692	10.21752	11	2056.4	25469.06
196	261.6421	10.19291	11	2077.6	25731.66
198	264.315	10.16869	11	2098.8	25994.26
200	266.9879	10.14484	11	2120	26256.87
202	269.6608	10.12136	11	2141.2	26519.47
204	272.3337	10.09823	11	2162.4	26782.07
206	275.0066	10.07546	11	2183.6	27044.67
208	277.6795	10.05302	11	2204.8	27307.27
210	280.3524	10.03091	11	2226	27569.88
212	283.0253	10.00912	11	2247.2	27832.48
214	285.6982	9.987652	10	2268.4	25540.98
216	288.3711	9.966485	10	2289.6	25779.71
218	291.044	9.945617	10	2310.8	26018.44
220	293.7169	9.925041	10	2332	26257.17
222	296.3898	9.904749	10	2353.2	26495.9
224	299.0627	9.884734	10	2374.4	26734.63
226	301.7356	9.864991	10	2395.6	26973.36
228	304.4085	9.845512	10	2416.8	27212.08
230	307.0814	9.826292	10	2438	27450.81
232	309.7543	9.807325	10	2459.2	27689.54
234	312.4272	9.788605	10	2480.4	27928.27
236	315.1001	9.770127	10	2501.6	28167
238	317.773	9.751885	10	2522.8	28405.73
240	320.4459	9.733874	10	2544	28644.46
242	323.1188	9.716089	10	2565.2	28883.19
244	325.7917	9.698525	10	2586.4	29121.92
246	328.4646	9.681178	10	2607.6	29360.65
248	331.1375	9.664043	10	2628.8	29599.37
250	333.8104	9.647114	10	2650	29838.1
252	336.4833	9.630389	10	2671.2	30076.83
254	339.1562	9.613863	10	2692.4	30315.56
256	341.8291	9.597532	10	2713.6	30554.29
258	344.502	9.581391	10	2734.8	30793.02
260	347.1749	9.565437	10	2756	31031.75
262	349.8478	9.549667	10	2777.2	31270.48
264	352.5207	9.534076	10	2798.4	31509.21
266	355.1936	9.518662	10	2819.6	31747.94
268	357.8665	9.50342	10	2840.8	31986.66
270	360.5394	9.488347	10	2862	32225.39
272	363.2123	9.47344	10	2883.2	32464.12
274	365.8852	9.458697	10	2904.4	32702.85
276	368.5581	9.444113	10	2925.6	32941.58
278	371.231	9.429686	10	2946.8	33180.31
280	373.9039	9.415413	10	2968	33419.04
282	376.5768	9.401291	10	2989.2	33657.77
284	379.2497	9.387318	10	3010.4	33896.5
286	381.9226	9.37349	10	3031.6	34135.23
288	384.5955	9.359805	10	3052.8	34373.95
290	387.2684	9.346261	10	3074	34612.68
292	389.9413	9.332855	10	3095.2	34851.41
294	392.6142	9.319584	10	3116.4	35090.14
296	395.2871	9.306446	10	3137.6	35328.87
298	397.96	9.293439	10	3158.8	35567.6
300	400.6329	9.280561	10	3180	35806.33
302	403.3058	9.267809	10	3201.2	36045.06
304	405.9787	9.255182	10	3222.4	36283.79
306	408.6516	9.242676	10	3243.6	36522.52
308	411.3245	9.230291	10	3264.8	36761.24
310	413.9974	9.218024	10	3286	36999.97
312	416.6703	9.205873	10	3307.2	37238.7
314	419.3432	9.193836	10	3328.4	37477.43
316	422.0161	9.181912	10	3349.6	37716.16
318	424.689	9.170098	10	3370.8	37954.89
320	427.3619	9.158393	10	3392	38193.62
322	430.0348	9.146795	10	3413.2	38432.35
324	432.7077	9.135302	10	3434.4	38671.08
326	435.3806	9.123913	10	3455.6	38909.81
328	438.0535	9.112626	10	3476.8	39148.53
330	440.7264	9.10144	10	3498	39387.26
332	443.3993	9.090353	10	3519.2	39625.99
334	446.0722	9.079363	10	3540.4	39864.72
336	448.7451	9.068468	10	3561.6	40103.45
338	451.418	9.057669	10	3582.8	40342.18
340	454.0909	9.046962	10	3604	40580.91
342	456.7638	9.036347	10	3625.2	40819.64
344	459.4367	9.025823	10	3646.4	41058.37
346	462.1096	9.015387	10	3667.6	41297.1
348	464.7825	9.005039	10	3688.8	41535.82
350	467.4554	8.994777	9	3710	37597.1
352	470.1283	8.9846	9	3731.2	37811.95
354	472.8012	8.974508	9	3752.4	38026.81
356	475.4741	8.964498	9	3773.6	38241.67
358	478.147	8.954569	9	3794.8	38456.52
360	480.8199	8.944721	9	3816	38671.38
362	483.4928	8.934952	9	3837.2	38886.23
364	486.1657	8.925261	9	3858.4	39101.09
366	488.8386	8.915647	9	3879.6	39315.95
368	491.5115	8.906109	9	3900.8	39530.8
370	494.1844	8.896646	9	3922	39745.66
372	496.8573	8.887257	9	3943.2	39960.52
374	499.5302	8.877941	9	3964.4	40175.37
376	502.2031	8.868697	9	3985.6	40390.23
378	504.876	8.859523	9	4006.8	40605.08
380	507.5489	8.85042	9	4028	40819.94
382	510.2218	8.841385	9	4049.2	41034.8
384	512.8947	8.832419	9	4070.4	41249.65
386	515.5676	8.82352	9	4091.6	41464.51
388	518.2405	8.814687	9	4112.8	41679.36
390	520.9134	8.80592	9	4134	41894.22
392	523.5863	8.797218	9	4155.2	42109.08
394	526.2592	8.788579	9	4176.4	42323.93
396	528.9321	8.780003	9	4197.6	42538.79
398	531.605	8.77149	9	4218.8	42753.64
400	534.2779	8.763037	9	4240	42968.5
402	536.9508	8.754646	9	4261.2	43183.36
404	539.6237	8.746314	9	4282.4	43398.21
406	542.2966	8.738042	9	4303.6	43613.07
408	544.9695	8.729828	9	4324.8	43827.93
410	547.6424	8.721671	9	4346	44042.78
412	550.3153	8.713572	9	4367.2	44257.64
414	552.9882	8.705529	9	4388.4	44472.49
416	555.6611	8.697541	9	4409.6	44687.35
418	558.334	8.689609	9	4430.8	44902.21
420	561.0069	8.68173	9	4452	45117.06
422	563.6798	8.673905	9	4473.2	45331.92
424	566.3527	8.666134	9	4494.4	45546.77
426	569.0256	8.658414	9	4515.6	45761.63
428	571.6985	8.650746	9	4536.8	45976.49
430	574.3714	8.64313	9	4558	46191.34
432	577.0443	8.635564	9	4579.2	46406.2
434	579.7172	8.628048	9	4600.4	46621.05
436	582.3901	8.620581	9	4621.6	46835.91
438	585.063	8.613163	9	4642.8	47050.77
440	587.7359	8.605793	9	4664	47265.62
442	590.4088	8.598471	9	4685.2	47480.48

One way to massively parallelize Solar Sim is to allow for many computers and have each run the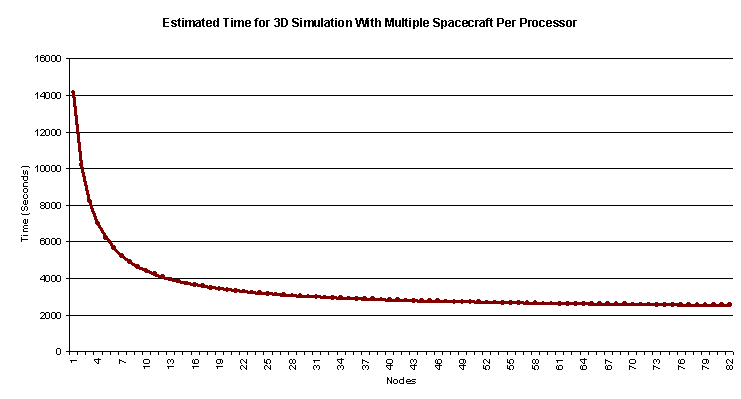
minimum process- the calculation of one spacecraft. However, since in some cases the transmission time will dwarf the calculation (as when there are huge numbers of computers increasing the delay time or a shorter simulation time) it is also important to look at how to balance the two factors of many computers with each computer calculating more spacecraft. This shows the calculation time when the work is shared evenly between all computers, as is used in this project.

The purpose of this analysis is to determine when the time benefits of adding a node are negligible. Each node costs money, time, and maintenance, plus boot time. When there are huge numbers of nodes but only a finite number of rockets the fixed delay transmission time will make the additional node only add to the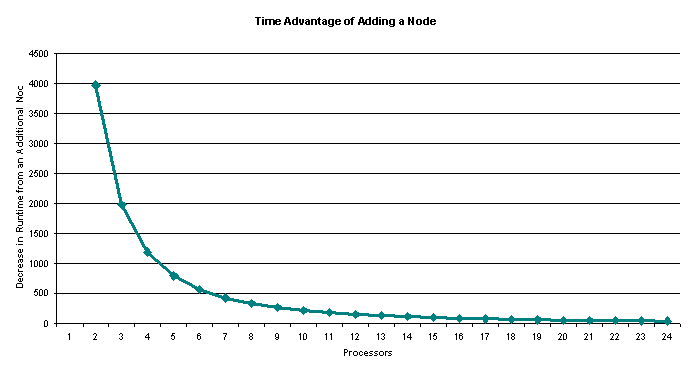
transmission wait without contributing to solving the problem faster. This graph shows the time improvement of adding another node (the derivative of the previous graph).

Raw data for 2D Solar Sim with multiple spacecraft per node:

n	trans time is (nodes-1)time delay plus send time	num sims= the negative of the log of desired width over log of rockets	celing function of the pervious	calc time= number of rockets times one calc over the nodes	total= (trans+calc)*sims
2	225	36.54121	37	1192.5	52447.5
3	225	23.05494	24	795	24480	27967.5
4	225	18.2706	19	596.25	15603.75	8876.25
5	225	15.73744	16	477	11232	4371.75
6	225	14.13607	15	397.5	9337.5	1894.5
7	225	13.01624	14	340.7143	7920	1417.5
8	225	12.1804	13	298.125	6800.625	1119.375
9	225	11.52747	12	265	5880	920.625
10	225	11	11	238.5	5098.5	781.5
11	225	10.56278	11	216.8182	4860	238.5
12	225	10.19291	11	198.75	4661.25	198.75
13	225	9.874829	10	183.4615	4084.615	576.6346
14	225	9.597532	10	170.3571	3953.571	131.044
15	225	9.353016	10	159	3840	113.5714
16	225	9.135302	10	149.0625	3740.625	99.375
17	225	8.939827	9	140.2941	3287.647	452.9779
18	225	8.763037	9	132.5	3217.5	70.14706
19	225	8.602126	9	125.5263	3154.737	62.76316
20	225	8.45484	9	119.25	3098.25	56.48684
21	225	8.319346	9	113.5714	3047.143	51.10714
22	225	8.19414	9	108.4091	3000.682	46.46104
23	225	8.077972	9	103.6957	2958.261	42.42095
24	225	7.969795	8	99.375	2595	363.2609
25	225	7.868721	8	95.4	2563.2	31.8
26	225	7.773998	8	91.73077	2533.846	29.35385
27	225	7.684979	8	88.33333	2506.667	27.17949
28	225	7.601105	8	85.17857	2481.429	25.2381
29	225	7.521892	8	82.24138	2457.931	23.49754
30	225	7.446917	8	79.5	2436	21.93103
31	225	7.37581	8	76.93548	2415.484	20.51613
32	225	7.308242	8	74.53125	2396.25	19.23387
33	225	7.243924	8	72.27273	2378.182	18.06818
34	225	7.1826	8	70.14706	2361.176	17.00535
35	225	7.124038	8	68.14286	2345.143	16.03361
36	225	7.068035	8	66.25	2330	15.14286
37	225	7.014404	8	64.45946	2315.676	14.32432
38	225	6.962979	7	62.76316	2014.342	301.3336
39	225	6.91361	7	61.15385	2003.077	11.26518
40	225	6.86616	7	59.625	1992.375	10.70192
41	225	6.820505	7	58.17073	1982.195	10.17988
42	225	6.776532	7	56.78571	1972.5	9.695122
43	225	6.734137	7	55.46512	1963.256	9.244186
44	225	6.693226	7	54.20455	1954.432	8.823996
45	225	6.653712	7	53	1946	8.431818
46	225	6.615515	7	51.84783	1937.935	8.065217
47	225	6.578562	7	50.74468	1930.213	7.722017
48	225	6.542785	7	49.6875	1922.813	7.400266
49	225	6.508121	7	48.67347	1915.714	7.098214
50	225	6.474511	7	47.7	1908.9	6.814286
51	225	6.441902	7	46.76471	1902.353	6.547059
52	225	6.410244	7	45.86538	1896.058	6.295249
53	225	6.37949	7	45	1890	6.057692
54	225	6.349596	7	44.16667	1884.167	5.833333
55	225	6.320522	7	43.36364	1878.545	5.621212
56	225	6.292229	7	42.58929	1873.125	5.420455
57	225	6.264683	7	41.84211	1867.895	5.230263
58	225	6.23785	7	41.12069	1862.845	5.049909
59	225	6.211699	7	40.42373	1857.966	4.878726
60	225	6.1862	7	39.75	1853.25	4.716102
61	225	6.161326	7	39.09836	1848.689	4.561475
62	225	6.137051	7	38.46774	1844.274	4.414331
63	225	6.113351	7	37.85714	1840	4.274194
64	225	6.090202	7	37.26563	1835.859	4.140625
65	225	6.067582	7	36.69231	1831.846	4.013221
66	225	6.045471	7	36.13636	1827.955	3.891608
67	225	6.02385	7	35.59701	1824.179	3.775441
68	225	6.002699	7	35.07353	1820.515	3.664399
69	225	5.982003	6	34.56522	1557.391	263.1234
70	225	5.961743	6	34.07143	1554.429	2.962733
71	225	5.941904	6	33.59155	1551.549	2.879276
72	225	5.922472	6	33.125	1548.75	2.799296
73	225	5.903432	6	32.67123	1546.027	2.722603
74	225	5.884771	6	32.22973	1543.378	2.649019
75	225	5.866475	6	31.8	1540.8	2.578378
76	225	5.848533	6	31.38158	1538.289	2.510526
77	225	5.830932	6	30.97403	1535.844	2.445318
78	225	5.813663	6	30.57692	1533.462	2.382617
79	225	5.796713	6	30.18987	1531.139	2.322298
80	225	5.780073	6	29.8125	1528.875	2.264241
81	225	5.763734	6	29.44444	1526.667	2.208333
82	225	5.747685	6	29.08537	1524.512	2.154472
83	225	5.731919	6	28.73494	1522.41	2.102557
84	225	5.716426	6	28.39286	1520.357	2.052496
85	225	5.701198	6	28.05882	1518.353	2.004202
86	225	5.686228	6	27.73256	1516.395	1.957592
87	225	5.671509	6	27.41379	1514.483	1.91259
88	225	5.657032	6	27.10227	1512.614	1.869122
89	225	5.642791	6	26.79775	1510.787	1.82712
90	225	5.628779	6	26.5	1509	1.786517
91	225	5.614991	6	26.20879	1507.253	1.747253
92	225	5.60142	6	25.92391	1505.543	1.709269
93	225	5.58806	6	25.64516	1503.871	1.672511
94	225	5.574905	6	25.37234	1502.234	1.636925
95	225	5.56195	6	25.10526	1500.632	1.602464
96	225	5.54919	6	24.84375	1499.063	1.569079
97	225	5.53662	6	24.58763	1497.526	1.536727
98	225	5.524235	6	24.33673	1496.02	1.505365
99	225	5.512029	6	24.09091	1494.545	1.474954
100	225	5.5	6	23.85	1493.1	1.445455
101	225	5.488142	6	23.61386	1491.683	1.416832
102	225	5.476451	6	23.38235	1490.294	1.389051
103	225	5.464923	6	23.15534	1488.932	1.362079
104	225	5.453554	6	22.93269	1487.596	1.335885
105	225	5.44234	6	22.71429	1486.286	1.31044
106	225	5.431278	6	22.5	1485	1.285714
107	225	5.420365	6	22.28972	1483.738	1.261682
108	225	5.409596	6	22.08333	1482.5	1.238318
109	225	5.398968	6	21.88073	1481.284	1.215596
110	225	5.388478	6	21.68182	1480.091	1.193495
111	225	5.378124	6	21.48649	1478.919	1.17199
112	225	5.367901	6	21.29464	1477.768	1.151062
113	225	5.357808	6	21.10619	1476.637	1.130689
114	225	5.347841	6	20.92105	1475.526	1.110852
115	225	5.337998	6	20.73913	1474.435	1.091533
116	225	5.328275	6	20.56034	1473.362	1.072714
117	225	5.318671	6	20.38462	1472.308	1.054377
118	225	5.309183	6	20.21186	1471.271	1.036506
119	225	5.299808	6	20.04202	1470.252	1.019086
120	225	5.290544	6	19.875	1469.25	1.002101
121	225	5.281389	6	19.71074	1468.264	0.985537
122	225	5.272341	6	19.54918	1467.295	0.969381
123	225	5.263397	6	19.39024	1466.341	0.953619
124	225	5.254555	6	19.23387	1465.403	0.938238
125	225	5.245814	6	19.08	1464.48	0.923226
126	225	5.237171	6	18.92857	1463.571	0.908571
127	225	5.228625	6	18.77953	1462.677	0.894263
128	225	5.220173	6	18.63281	1461.797	0.88029
129	225	5.211814	6	18.48837	1460.93	0.866642
130	225	5.203545	6	18.34615	1460.077	0.853309
131	225	5.195366	6	18.20611	1459.237	0.840282
132	225	5.187275	6	18.06818	1458.409	0.82755
133	225	5.179269	6	17.93233	1457.594	0.815106
134	225	5.171348	6	17.79851	1456.791	0.80294
135	225	5.16351	6	17.66667	1456	0.791045
136	225	5.155753	6	17.53676	1455.221	0.779412
137	225	5.148076	6	17.40876	1454.453	0.768033
138	225	5.140477	6	17.28261	1453.696	0.756903
139	225	5.132956	6	17.15827	1452.95	0.746012
140	225	5.12551	6	17.03571	1452.214	0.735355
141	225	5.118138	6	16.91489	1451.489	0.724924
142	225	5.110839	6	16.79577	1450.775	0.714714
143	225	5.103613	6	16.67832	1450.07	0.704718
144	225	5.096456	6	16.5625	1449.375	0.69493
145	225	5.089369	6	16.44828	1448.69	0.685345
146	225	5.082351	6	16.33562	1448.014	0.675957
147	225	5.075399	6	16.22449	1447.347	0.66676
148	225	5.068513	6	16.11486	1446.689	0.65775
149	225	5.061692	6	16.00671	1446.04	0.648921
150	225	5.054935	6	15.9	1445.4	0.640268
151	225	5.048241	6	15.7947	1444.768	0.631788
152	225	5.041608	6	15.69079	1444.145	0.623475
153	225	5.035036	6	15.58824	1443.529	0.615325
154	225	5.028524	6	15.48701	1442.922	0.607334
155	225	5.02207	6	15.3871	1442.323	0.599497
156	225	5.015675	6	15.28846	1441.731	0.591811
157	225	5.009336	6	15.19108	1441.146	0.584272
158	225	5.003054	6	15.09494	1440.57	0.576877
159	225	4.996827	5	15	1200	240.5696
160	225	4.990654	5	14.90625	1199.531	0.46875
161	225	4.984535	5	14.81366	1199.068	0.462927
162	225	4.978468	5	14.72222	1198.611	0.457212
163	225	4.972454	5	14.6319	1198.16	0.451602
164	225	4.96649	5	14.54268	1197.713	0.446095
165	225	4.960577	5	14.45455	1197.273	0.440687
166	225	4.954714	5	14.36747	1196.837	0.435378
167	225	4.948899	5	14.28144	1196.407	0.430164
168	225	4.943133	5	14.19643	1195.982	0.425043
169	225	4.937414	5	14.11243	1195.562	0.420013
170	225	4.931743	5	14.02941	1195.147	0.415071
171	225	4.926117	5	13.94737	1194.737	0.410217
172	225	4.920537	5	13.86628	1194.331	0.405447
173	225	4.915002	5	13.78613	1193.931	0.40076
174	225	4.90951	5	13.7069	1193.534	0.396153
175	225	4.904063	5	13.62857	1193.143	0.391626
176	225	4.898659	5	13.55114	1192.756	0.387175
177	225	4.893297	5	13.47458	1192.373	0.3828
178	225	4.887976	5	13.39888	1191.994	0.378499
179	225	4.882698	5	13.32402	1191.62	0.37427
180	225	4.877459	5	13.25	1191.25	0.370112
181	225	4.872261	5	13.1768	1190.884	0.366022
182	225	4.867103	5	13.1044	1190.522	0.362
183	225	4.861984	5	13.03279	1190.164	0.358044
184	225	4.856903	5	12.96196	1189.81	0.354152
185	225	4.85186	5	12.89189	1189.459	0.350323
186	225	4.846855	5	12.82258	1189.113	0.346556
187	225	4.841887	5	12.75401	1188.77	0.34285
188	225	4.836955	5	12.68617	1188.431	0.339202
189	225	4.83206	5	12.61905	1188.095	0.335613
190	225	4.8272	5	12.55263	1187.763	0.33208
191	225	4.822376	5	12.48691	1187.435	0.328603
192	225	4.817586	5	12.42188	1187.109	0.32518
193	225	4.812831	5	12.35751	1186.788	0.32181
194	225	4.808109	5	12.29381	1186.469	0.318493
195	225	4.803421	5	12.23077	1186.154	0.315226
196	225	4.798766	5	12.16837	1185.842	0.312009
197	225	4.794143	5	12.1066	1185.533	0.308842
198	225	4.789553	5	12.04545	1185.227	0.305722
199	225	4.784995	5	11.98492	1184.925	0.30265
200	225	4.780468	5	11.925	1184.625	0.299623
201	225	4.775972	5	11.86567	1184.328	0.296642
202	225	4.771507	5	11.80693	1184.035	0.293705
203	225	4.767072	5	11.74877	1183.744	0.290811
204	225	4.762667	5	11.69118	1183.456	0.28796
205	225	4.758292	5	11.63415	1183.171	0.285151
206	225	4.753946	5	11.57767	1182.888	0.282382
207	225	4.749629	5	11.52174	1182.609	0.279654
208	225	4.745341	5	11.46635	1182.332	0.276965
209	225	4.74108	5	11.41148	1182.057	0.274315
210	225	4.736848	5	11.35714	1181.786	0.271702
211	225	4.732643	5	11.30332	1181.517	0.269127
212	225	4.728466	5	11.25	1181.25	0.266588
213	225	4.724316	5	11.19718	1180.986	0.264085
214	225	4.720192	5	11.14486	1180.724	0.261616
215	225	4.716094	5	11.09302	1180.465	0.259183
216	225	4.712023	5	11.04167	1180.208	0.256783
217	225	4.707978	5	10.99078	1179.954	0.254416
218	225	4.703958	5	10.94037	1179.702	0.252082
219	225	4.699963	5	10.89041	1179.452	0.24978
220	225	4.695993	5	10.84091	1179.205	0.247509
221	225	4.692048	5	10.79186	1178.959	0.245269
222	225	4.688127	5	10.74324	1178.716	0.24306
223	225	4.68423	5	10.69507	1178.475	0.24088
224	225	4.680357	5	10.64732	1178.237	0.238729
225	225	4.676508	5	10.6	1178	0.236607
226	225	4.672682	5	10.5531	1177.765	0.234513
227	225	4.668879	5	10.50661	1177.533	0.232447
228	225	4.665099	5	10.46053	1177.303	0.230408
229	225	4.661342	5	10.41485	1177.074	0.228396
230	225	4.657607	5	10.36957	1176.848	0.22641
231	225	4.653894	5	10.32468	1176.623	0.224449
232	225	4.650203	5	10.28017	1176.401	0.222515
233	225	4.646534	5	10.23605	1176.18	0.220605
234	225	4.642886	5	10.19231	1175.962	0.218719
235	225	4.63926	5	10.14894	1175.745	0.216858
236	225	4.635654	5	10.10593	1175.53	0.21502
237	225	4.63207	5	10.06329	1175.316	0.213205
238	225	4.628506	5	10.02101	1175.105	0.211414
239	225	4.624962	5	9.979079	1174.895	0.209645
240	225	4.621439	5	9.9375	1174.688	0.207897
241	225	4.617935	5	9.896266	1174.481	0.206172
242	225	4.614451	5	9.855372	1174.277	0.204468
243	225	4.610987	5	9.814815	1174.074	0.202785
244	225	4.607542	5	9.77459	1173.873	0.201123
245	225	4.604117	5	9.734694	1173.673	0.199481
246	225	4.60071	5	9.695122	1173.476	0.19786
247	225	4.597323	5	9.65587	1173.279	0.196258
248	225	4.593954	5	9.616935	1173.085	0.194675
249	225	4.590603	5	9.578313	1172.892	0.193111
250	225	4.587271	0	9.54	0	0.191566

Cellular Automata Results

The cellular automata program simulates the Game of Life for 1000 timesteps, requiring 20 transmissions because of the 50 pixel boundary size. Each data point shows the time each node took to calculate its portion of the simulation field. 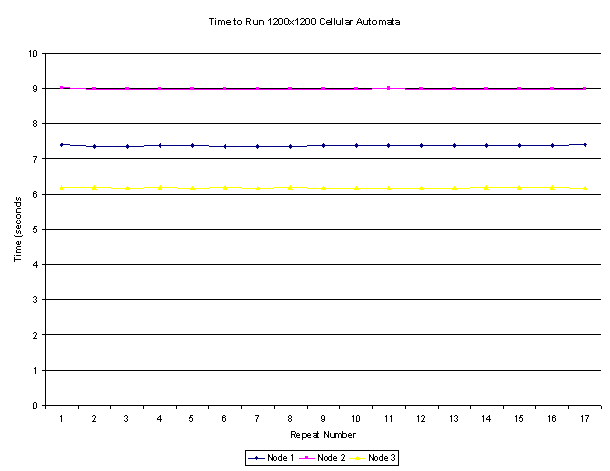Raw data for cellular automata performance:

node	1	2	3
rows	410	400	530
	7.39	9.01	6.189
	7.37	8.99	6.189
	7.37	8.99	6.179
	7.38	8.99	6.189
	7.38	8.98	6.179
	7.37	8.98	6.189
	7.37	8.98	6.179
	7.37	8.99	6.188
	7.381	8.99	6.179
	7.381	8.99	6.179
	7.381	9	6.179
	7.381	8.99	6.179
	7.381	8.99	6
	7.381	8.99	6.189
	7.381	8.99	6.189
	7.381	8.99	6.189
	7.391	8.99	6.179
sum	125.439	152.83	105.122
average per time	7.378764706	8.99	6.183647059
average per pixel	0.000122979	1.87292E-05	9.72272E-06
total time	194.089	195.501	192.377
total calc average	5.04771E-05

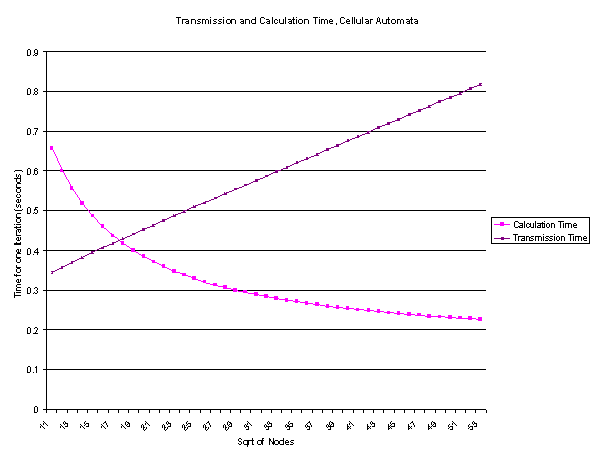
The calculation time vs. transmission time remained the vital factor in total runtime. Note that the nodes are in an array, meaning that when the x-axis reads 13 nodes it means there is an array with 13 nodes on a side.

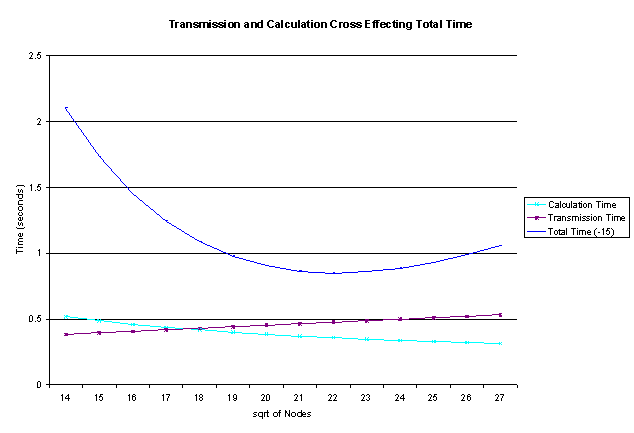
This shows the effect transmission and calculation have on the total time to calculate. Calculation time has been scaled back so as to compare.

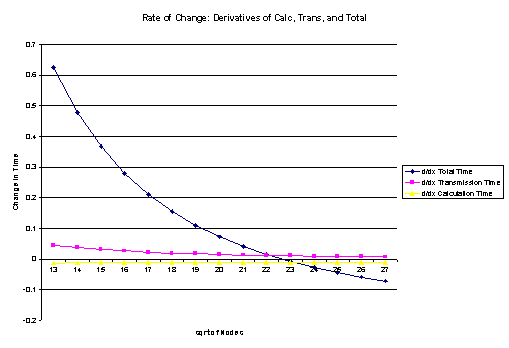
Why does the lowest value of total time not correspond with the cross of calculation time and transmission time? As shown is the next graph, this is a result of the first derivative of the data, not the magnitude.

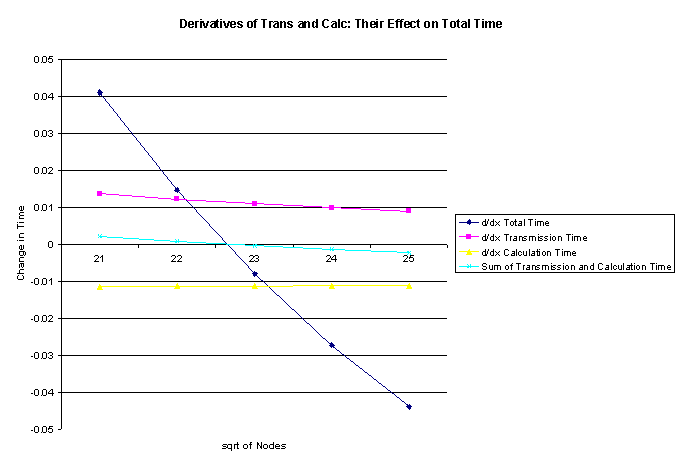
To further illustrate this point, the sum of the derivatives of transmission time and calculation time intersect total time’s derivative at 0.

Raw data for fractal performance model:

I	j	ni	nj	B (boarder width)	c (calc time 1 pixel)	e(x) is send of x pixels
1200	1200	3	1	50	1.5E-05	1.08E-06
calculation time (single)	9.760833
transmission (single)	0.259906
interactions (how many sends)	20
total time (repeats*transmission+calculation)	200.4148		normal (for one computer)	21624
	3.340246
nodes	calc	t1	t2	trans	inter	total
1	25.37817	0.064976	0.070391	0	20	482.1852
2	7.358167	0.032488	0.037903	0.140782	20	142.48
3	3.754167	0.021659	0.027074	0.194929	20	75.03282
4	2.402667	0.016244	0.021659	0.227417	20	49.9716
5	1.735927	0.012995	0.01841	0.251242	20	37.75621
6	1.3515	0.010829	0.016244	0.270735	20	30.82247
7	1.10633	0.009282	0.014697	0.287753	20	26.48757
8	0.938542	0.008122	0.013537	0.303223	20	23.59353
9	0.817574	0.00722	0.012634	0.317662	20	21.56949
10	0.726807	0.006498	0.011912	0.33138	20	20.10554
11	0.656514	0.005907	0.011322	0.344572	20	19.02063
12	0.600667	0.005415	0.010829	0.35737	20	18.2027
13	0.55535	0.004998	0.010413	0.369866	20	17.5791
14	0.517922	0.004641	0.010056	0.382123	20	17.10085
15	0.48654	0.004332	0.009746	0.39419	20	16.73387
16	0.459885	0.004061	0.009476	0.406103	20	16.45377
17	0.43699	0.003822	0.009237	0.417887	20	16.24267
18	0.41713	0.00361	0.009025	0.429566	20	16.08722
19	0.399751	0.00342	0.008835	0.441156	20	15.97723
20	0.384427	0.003249	0.008664	0.452669	20	15.90482
21	0.37082	0.003094	0.008509	0.464117	20	15.8638
22	0.358663	0.002953	0.008368	0.475509	20	15.84926
23	0.347739	0.002825	0.00824	0.486852	20	15.85724
24	0.337875	0.002707	0.008122	0.498152	20	15.88452
25	0.328925	0.002599	0.008014	0.509415	20	15.92846
26	0.32077	0.002499	0.007914	0.520644	20	15.98687
27	0.313311	0.002407	0.007821	0.531844	20	16.05794
28	0.306463	0.002321	0.007735	0.543017	20	16.14011
29	0.300155	0.002241	0.007655	0.554167	20	16.2321
30	0.294327	0.002166	0.007581	0.565295	20	16.33281
31	0.288926	0.002096	0.007511	0.576404	20	16.44127
32	0.283909	0.002031	0.007445	0.587495	20	16.55667
33	0.279236	0.001969	0.007384	0.59857	20	16.67831
34	0.274873	0.001911	0.007326	0.609632	20	16.80558
35	0.27079	0.001856	0.007271	0.620679	20	16.93792
36	0.266963	0.001805	0.00722	0.631715	20	17.07488
37	0.263368	0.001756	0.007171	0.64274	20	17.21603
38	0.259984	0.00171	0.007125	0.653754	20	17.36101
39	0.256794	0.001666	0.007081	0.664759	20	17.5095
40	0.253782	0.001624	0.007039	0.675755	20	17.66119
41	0.250933	0.001585	0.006999	0.686742	20	17.81583
42	0.248235	0.001547	0.006962	0.697723	20	17.97319
43	0.245676	0.001511	0.006926	0.708696	20	18.13306
44	0.243245	0.001477	0.006891	0.719663	20	18.29525
45	0.240934	0.001444	0.006859	0.730624	20	18.45959
46	0.238734	0.001413	0.006827	0.741578	20	18.62593
47	0.236637	0.001382	0.006797	0.752528	20	18.79413
48	0.234635	0.001354	0.006768	0.763473	20	18.96405
49	0.232724	0.001326	0.006741	0.774413	20	19.13559
50	0.230896	0.0013	0.006714	0.785348	20	19.30864
51	0.229147	0.001274	0.006689	0.796279	20	19.4831
52	0.227471	0.00125	0.006664	0.807207	20	19.65889
53	0.225865	0.001226	0.006641	0.818131	20	19.83591

f (sim steps)	t1 (hotizontal send)	t2 (vertical send)
1000	0.064976	0.027074

dervat of total	dervat of trans	dervat of calc	sum of trans and calc
0.623601	0.045317	-0.0125	0.032821
0.478247	0.037428	-0.01226	0.025171
0.36698	0.031382	-0.01207	0.019315
0.280103	0.026655	-0.01191	0.014742
0.211095	0.022895	-0.01178	0.01111
0.155454	0.019861	-0.01168	0.008182
0.109993	0.017378	-0.01159	0.005789
0.072411	0.015324	-0.01151	0.003811
0.041016	0.013607	-0.01145	0.002159
0.014539	0.012157	-0.01139